Studying Relationships Among w, pi, i, e, and one other Mathematical Constant

It’s Friday, so it’s another recreational mathematical journey. Get ready for another surprise or two relating to w

So far, in this journey, we have seen that in addition to providing unique functions for the nth root of any number, including the square root, we can, using w, also find ways to

• Express 𝜋 as 𝜋=5*arccos⁡*((w(1+sqrt(5))/ln(10))

• Find the area of circle without using π

• Find the area under a hyperbola.

Mathematicians love elegance. That’s why some see Euler’s identity as the most beautiful equation in the world. It reads:

e^(i𝜋)+1 = 0

- e: Euler's number is approximately equal to 2.71828. It is the base of the natural logarithm and is fundamental in studying exponential growth and decay.

- i: The imaginary unit, defined by the property i^2 = -1, or sqrt(-1). It is essential in complex number theory.

- 𝜋: Pi, approximately equal to 3.14159. It is the ratio of the circumference of a circle to its diameter.

- 1 and 0: Fundamental constants representing the multiplicative and additive identities, respectively.

Euler's identity is remarkable because it links five of the numbers considered by some in mathematics to be among the most important, including 1 (the multiplicative identity), 0 (the additive identity), and, as above, e (the base of the natural logarithm), i (the imaginary unit), 𝜋 (the circle constant).

The identity is a special case of Euler's formula, which is:

e^(ix) = cos(x) + isin(x)

When x = 𝜋:

e^(i𝜋) = cos(𝜋) + isin(𝜋)

Since cos(pi) = -1 and sin(pi) = 0:

e^(i𝜋) = -1

Adding 1 to both sides gives Euler's identity:

e^(i𝜋) + 1 = 0

Neat trick!

Among these special numbers, I have found the following relationships

𝜋=5*arccos⁡*((w(1+sqrt(5))/ln(10))

Rather non-canonically, I admit, but:

• i = (e^(i*ln(10)/4) - cos(ln(10)/4))/sin(ln(10)/4)

• i = (e^(i*w) - cos(w))/sin(w)

Anyone exploring this will say “where are the imaginary and real parts?”; sin(w) cancels sin(w) on that journey, leaving i.

Another neat trick, try it out.

And also:

• e = (sin(w)*(cot(w) + i))^(-i/w)

• Of course, e = 10^(1/(4w)) because w = ln(10)/4.

This week, I found one more…

Φ = (1+e^((ln(5)/ln(10))*2*w))/2 … precisely.

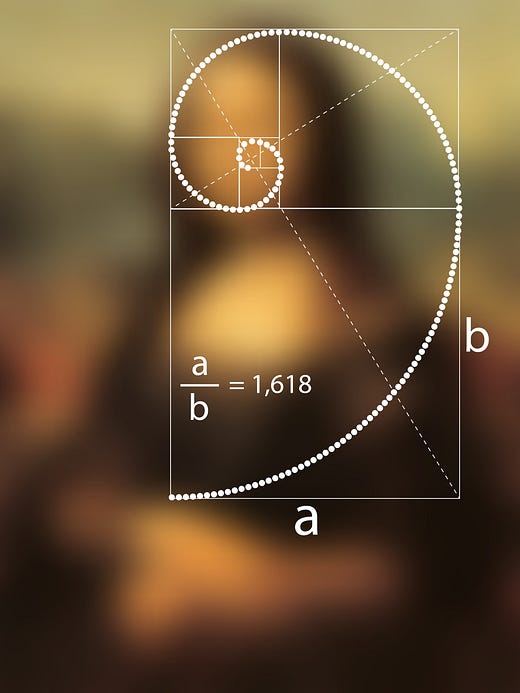
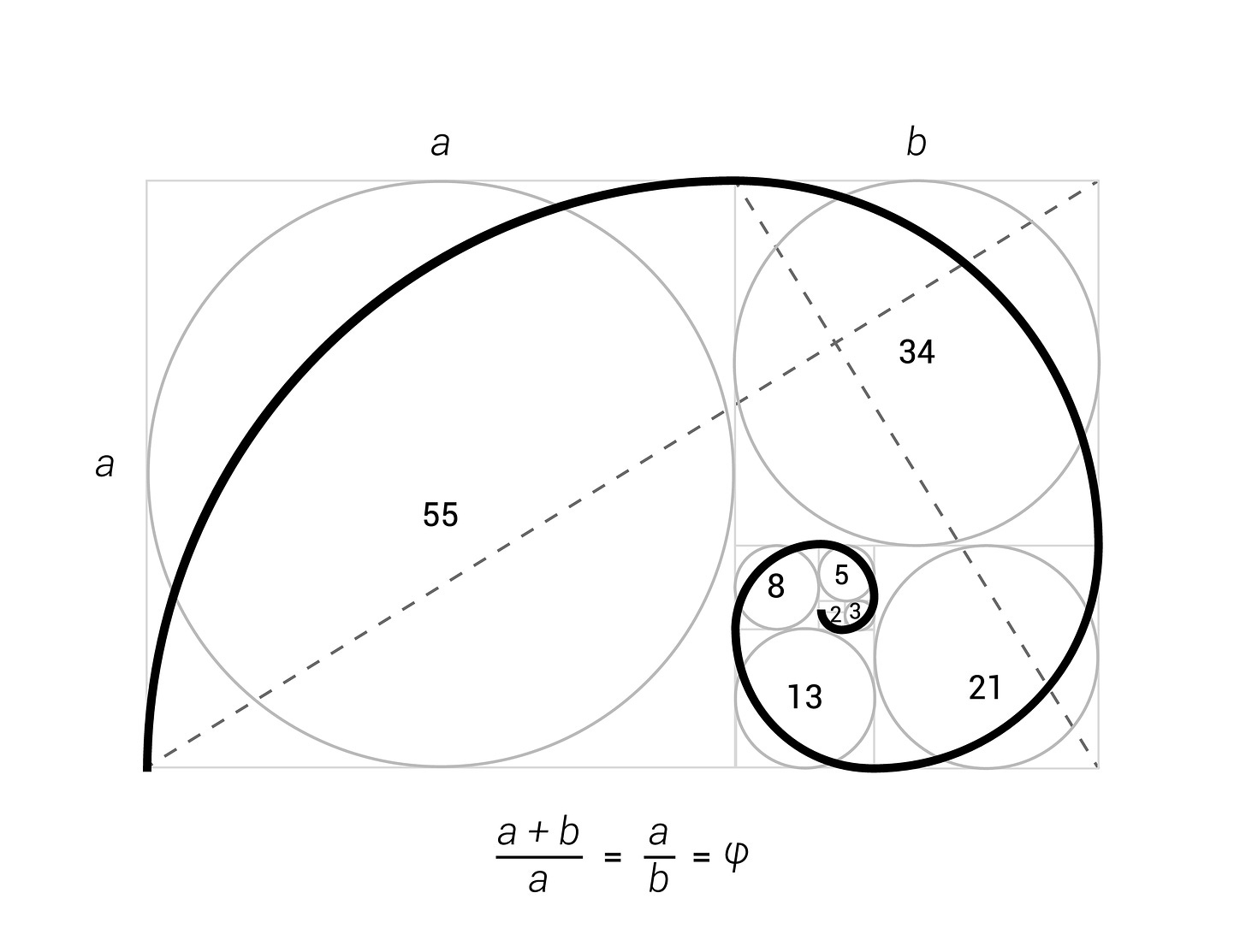
The golden ratio, often denoted by the Greek letter Phi (Φ) (uppercase) or ϕ (lowercase), is an irrational number that approximately equals 1.6180339887... The golden ratio is recognized as a symbol of harmony and beauty, revered for its appearance in patterns in the natural world and human-made structures. It is a unique and fascinating mathematical constant studied for thousands of years due to its appearance in various natural phenomena, art, architecture, and financial markets.

The golden ratio is defined algebraically as

Φ= (1+sqrt(5))/2

If you divide a line into two parts such that the ratio of the whole line to the longer part is the same as the ratio of the longer part to the shorter part, that ratio is the golden ratio, denoted by Φ.

In other words, if a line segment is divided into a longer part (a) and a shorter part (b), the golden ratio is achieved when:

(a+b)/a = a/b = Φ.

Interestingly, this week's explorations showed that Φ can also be expressed using logarithms and exponents, showing its deep connections within mathematics.

and via logarithms and exponentials using w as

Φ = (1+e^((ln(5)/ln(10))*2*w))/2 … precisely.

[Excel for Excel checkers: = (1 + EXP((LN(5) / LN(10)) * 2 * (LN(10)/4)))/2) ]

This versatility and recurring appearance of Φ and w in different domains make things interesting. Via simplification, the exponent is ln(5)/2, so

Φ = 1+e^(ln(5)/2)

and of course

Φ= (1+sqrt(5))/2

Some will say that w adds nothing, but I disagree. They are overlooking the entire exercise. I believe looking at the world of maths via w points to a unique modulator that can, in some circumstances, allow us to see (recognize) ways to move among various domains of mathematics with relative ease, given the alternative mathematical operations involved.

Raising the Stakes: Avoiding the Entropy of Mathematics

One thing that we must agree on is that w is found in many interesting places and can be used with some dexterity across many areas of mathematical inquiry. It’s not elegant, but it avoids what I call “the entropy of mathematics”. The entropy of mathematics is the decay of information and nuance in complex systems that occurs when simplification removes essential complexity. Elegance, beauty, and simplicity cause wonder and joy in surprisingly simple equations that are correct. Yes, it can be reassuring. However, the universe is complex, and humans do not yet know - and may never know - all the dimensions by or in which objects are characterized. So, canceling out things with the same units can potentially lead to simpler, seemingly correct equations that have lost some information.

Now for the bold part.

Hypothesis: Some numbers of the form ln(x)/y will point to infinitely many unique modulators that will prove useful in mapping problems across maths. I speculate that solution sets may be found and the likelihood of a solution being found using harmonic series; they should tend to be found on multiples of x (but not every multiple of x).

I am studying a framework for evaluating/exploring this hypothesis.

If this is correct, then given the unique utility of w in efforts to study and connect e, i, π, and Φ, w may be seen to hold a special place in the mathematical landscape. Its role as a modulator and its connections to fundamental constants suggest that w is not just an interesting constant but also a profoundly fundamental one that enriches our understanding of various mathematical domains.

One could argue that w is a cornerstone in exploring mathematical relationships and, certainly, for learning beyond the basics in teaching advanced maths and their relationships.

One could also argue that because w can be used to study and understand e, i, π, and Φ, that w may be for species who use base 10 mathematics, and is quite fundamental after all.

Sign up for this course w/Dr. Lyons-Weiler in the Fall of 2024, and go deep into analytics and hear some seemingly outlandish, non-traditional, but thought-provoking ideas. Monthly payment options are available, contact info@ipak-edu.org