Modern Esoterica Series: The Poverty of the Polynomial

Linear modeling has had us searching for coefficient parameter estimates with occasional interaction terms for decades. Here I show the poverty of the polynomial with a lesson for over 90% of science.

This is the first in a series of articles on Popular Rationalism that are based on mathematical meanderings that (1) I have conducted for the sake of it, usually when I’m bored, and (2) Have blown my mind, and will, I hope, do to the same for you.

If the goal of science is understanding, 240 years of linear modeling has left us like babes in the dark wilderness. The palliations students are offered are poor excuses for an the incompleteness of model selection.

Linear systems modeling (such as Generalized Linear Modeling, of which linear regression would be a particular form) has had us doing error minimizing curve-fitting of one type of the other since the early 19th century. The development and use of multiple regression in scientific studies have increased from near nil in the early 1970’s to the point where 1.2% of articles in Pubmed journals that mention “Journal” mention “multiple regression”.

Y = (%) = # Articles that mention “Multiple Regression” / # Articles that mention “Journal” per year

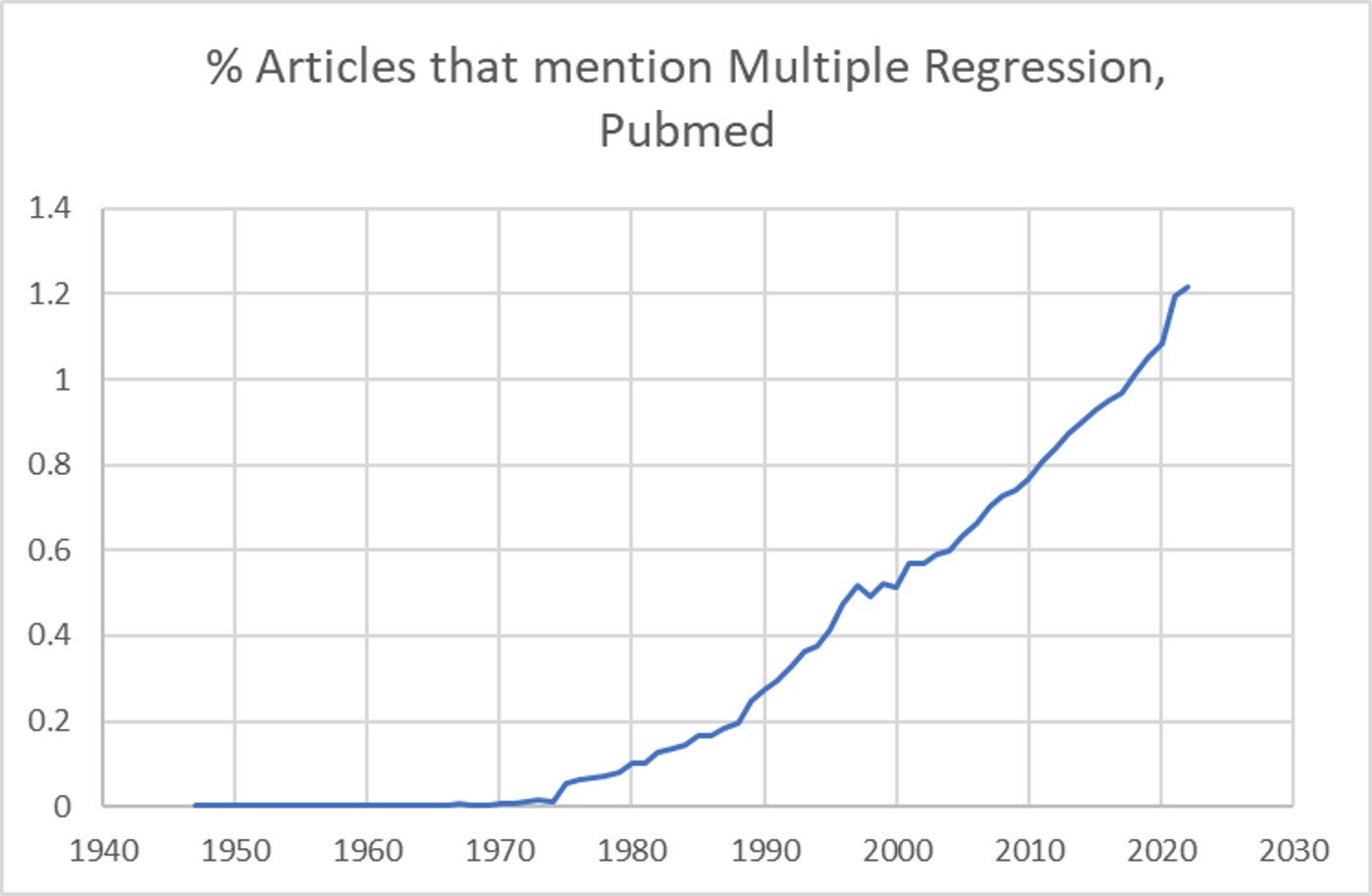
Due to the propagation of information throughout scientific communities, I estimate that over 90% of science conducted has been impacted by findings from multiple regression or other types of linear models.

One of my complaints about multiple regression - and any form of linear modeling, even simple linear regression - has always been that it has been abused as providing an assessment of both “predictive power” and “explanatory power”. The first claim is bogus because predictions using new data are nearly never done, and the fact that the study data fits itself well is a tautology.

In contrived, man-made contexts, where the input variables (usually X’s) are known, one can study the relative contribution in a descriptive manner using GLMs. One can also study, given the correct study design, whether any two X’s seem to interact in an important, synergistic manner. But getting “understanding” this way is fraught with risk, as we will see.

A multiple regression model, such as the standard

Y-hat = m1x1 + m2x2 + m3x3…mnxn (Eqn 1)

is used to assess, given a measure of the goodness of fit of predicted values of Y (Y-hat) to some empirical data. The slopes m1, m2, m3…mn are also known as coefficients, can each be studied for statistical significance, as can any of their interaction terms, i.e., m1 x m2. The x’s in the equation are the given empirical values of any xi meant to be used as inputs to calculate the predicted value of Y (Y-hat) given a single value of xi (for simple linear regression) or a vector X of {x1, x2, x3…xn}. How and why particular variables are selected to be included in X usually involves some odd mixture of background knowledge, luck, and funding availability.

A multiple regression such as Eqn 1 is technically a polynomial, and any x could also have a power value (as in x^2, or x-squared), if the modeler is aware of that type of functional relationship.

When I get bored I like to throw away all of the strictures of mathematics and cast my line far and deep into the unknown universe of numbers and objects (NAO’s). As part of my Modern Esoterica project, I have conjured methods for determining the square root of any number with an equation using a likely new transcendental number important to trigonometry and the geometry of circles. I have found patterns in the digits of transcendental numbers. I have studied the space between real and imaginary numbers. It’s wild.

Few people realize that the factoring and guesswork we did in our grammar school math classes to find square roots were inexact approximations methods that, to the uninitiated, only felt like math. But that process was not formal math, with axioms and proofs. It was a taste of independent thought in the area of numbers and objects, and an introduction to giving ourselves permission to attempt to problem-solve.

WARNING: DRAGONS AHEAD, TURN BACK NOW

What I’m about to show you will rattle your cage if you’re an academic who is used to thinking in terms of multiple regression models or GLMs. Given a pair of paired vectors X and Y, it is widely known that it is a bit foolhardy to attempt to infer any particular functional meaning to coefficients and exponent values found in polynomial equations fitting a non-linear curve. If you plot your Y’s against your X’s, and look at the result, then try to fit a polynomial, your brain likely thinks “That’s non-linear, perhaps a single exponent will do. That leads to a binomial equation, so I’ll expect something like Y = ax + bx^2”.

As tempting as that might be, somewhere in your head is a missive from a mentor, “Tsk, tsk, tsk, that’s a no-no. That’s just curve-fitting, and you can’t interpret the coefficients and exponents. Extrapolations don’t do well under polynomial guesswork” or similar.

If you’ve never heard that, now you have, and I’m that mentor.

None of that is earth-shattering. But check out this contention:

Multiple regression is polynomial curve-fitting (most often without the exponents).

Whoa.

Don’t believe me? It’s not too late. Turn back while you can.

The Paradox of the Arbitrary Polynomials Experiment

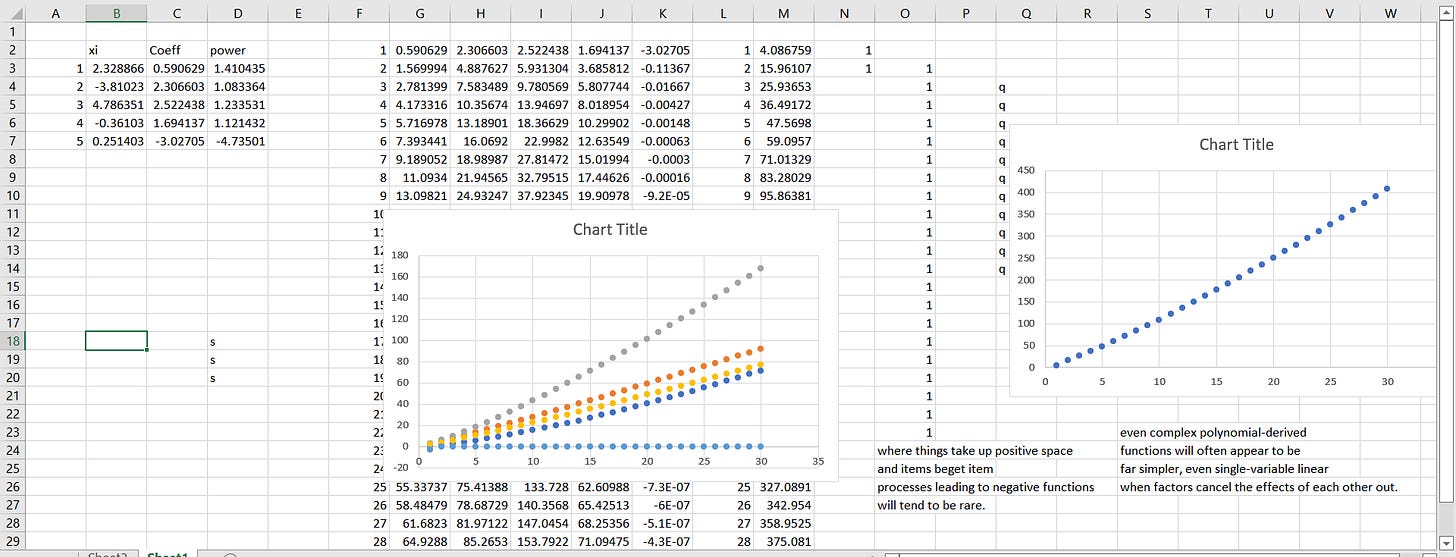
I set up a numerical experiment in which I generated five (5) random, fixed x’s, five random coefficients, and five exponents for five set of model inputs, and generated curves as simple additive functions of a five-variable generative model.

To be clear: Each run of this experiment results in five sets of xi’s, coefficients, and exponents.

What might one expect of such a complex generative model?

Well, we should expect additive effects only; the model had no interactions. Every one of the inputs was both random, and independent. (For exacting number scientists, they were pseudorandomly generated, but this is for descriptive purposes).

As each iteration of the model was thrown, a full model was plotted. I saw nonlinear curves, some increasing, and some decreasing. I expected that.

But what I saw after my fifth throw of the model chilled me to my bones.

Here. I’ll just show it to you.

Fiver factors as inputs, and yet anyone seeing the data would model with a simple linear regression (data on the right). The truth is on the left: each variable has its own input.

I’ll wait a spell for you to catch your breath. When the penny drops, read on.

I know, right? Multiple regression hits different now, right?

Just in case anyone thinks “Well that’s expected, it’s an additive model, and variance might be expected due to trade-offs…”

Ready? I don’t think you are.

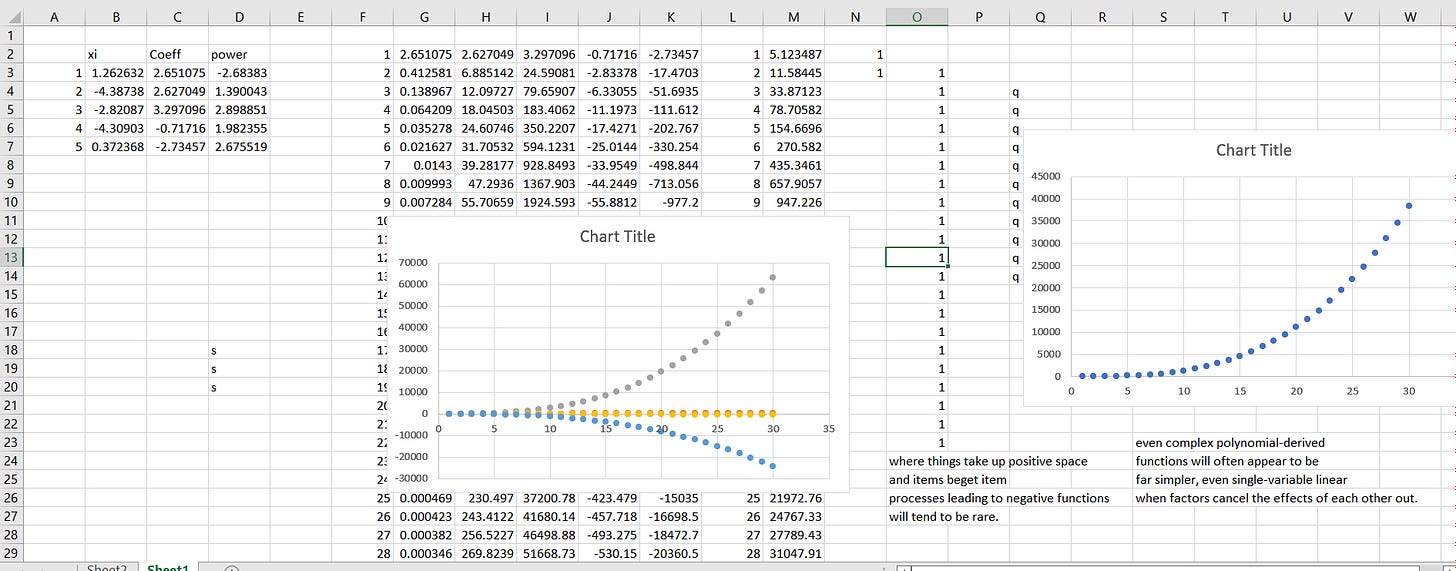
On the right is the output of the composite model.

On the left? Each individual function of each contributing variable.

The data the scientist would see in on the right. On the left, we see the deconvolved truth. If the variable with the decreasing function was unknown, the data might still be a perfect fit for an exponential increase in Y given an increase in X, per the data the scientist has at hand. They would have a very tight fight, and not impetus to search further. But the simple linear model parameters would all be way off.

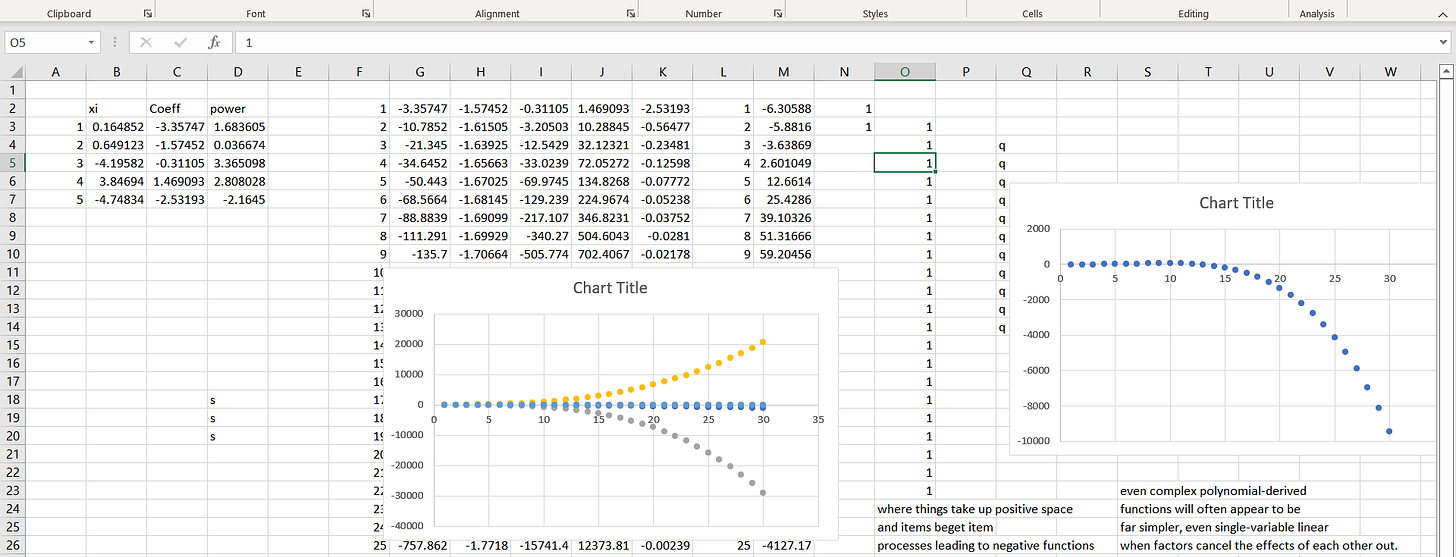
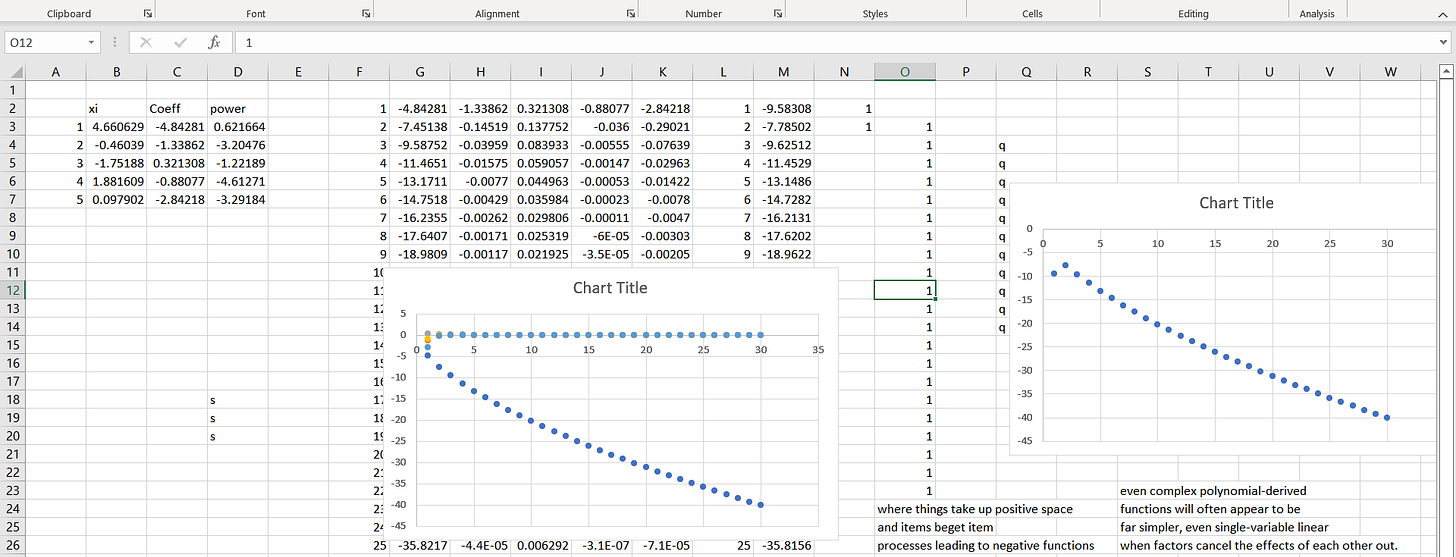
Let’s consider another throw:

No one - I mean no one - would think given a strong non-linear (negative) nose dive in empirical empirical data between X and Y (right) and a strong - nearly as strong - positive relationship hidden in an unmeasured variable in the opposite direction.

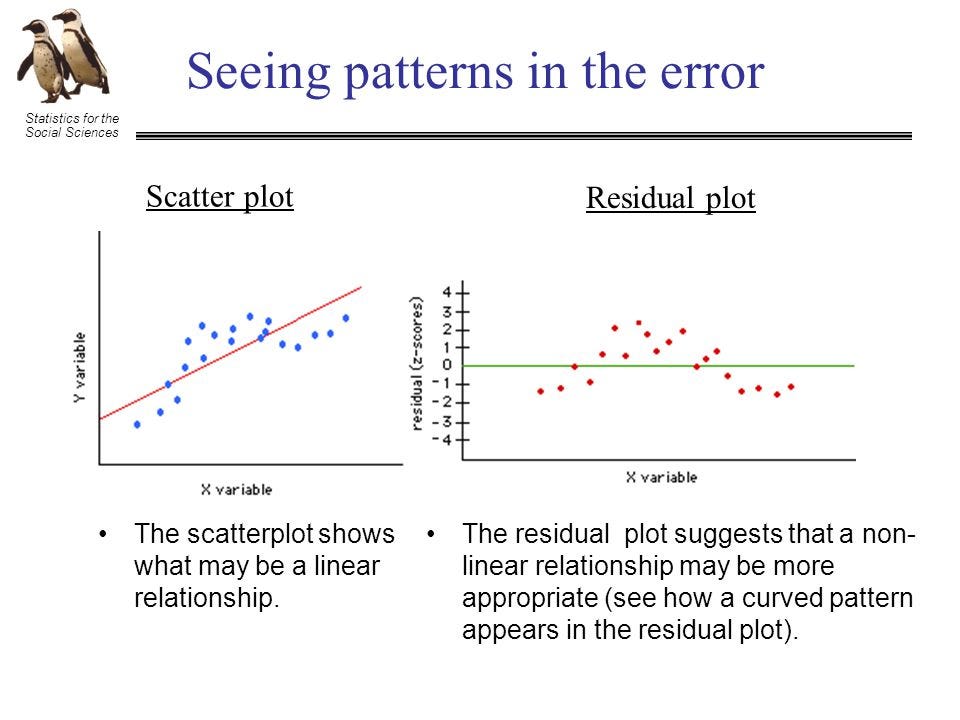
Those experienced with regression will (correctly) point out that we can alway study the residual plots, as is explained by this graph from the presentation (“Statistics for the Social Science”:

“Suggests” a non-linear relationship “may” be more appropriate. Fine. Multiply this process by the hundreds of thousands of researchers examining residual plots. What is the false discovery rate? How often do we follow our noses down blind alleys?

I’m becoming increasingly convinced that the problem of reproducibility in science is heavily influenced by a lack of skepticism and independent thought or inquisitiveness or, frankly, courage on people doing linear modeling in science. They rarely know anything about model space. One missed critical parameter in the linear modeling paradigm, and we’re done for. Most if not all of the coefficient values (optimized by least-squares) will be truly far off within a given study - and there is no robust way to check ourselves. So we publish. And we accept palliations akin to “models may vary”.

Remember those trade-offs that you hoped to use to brush off problems?

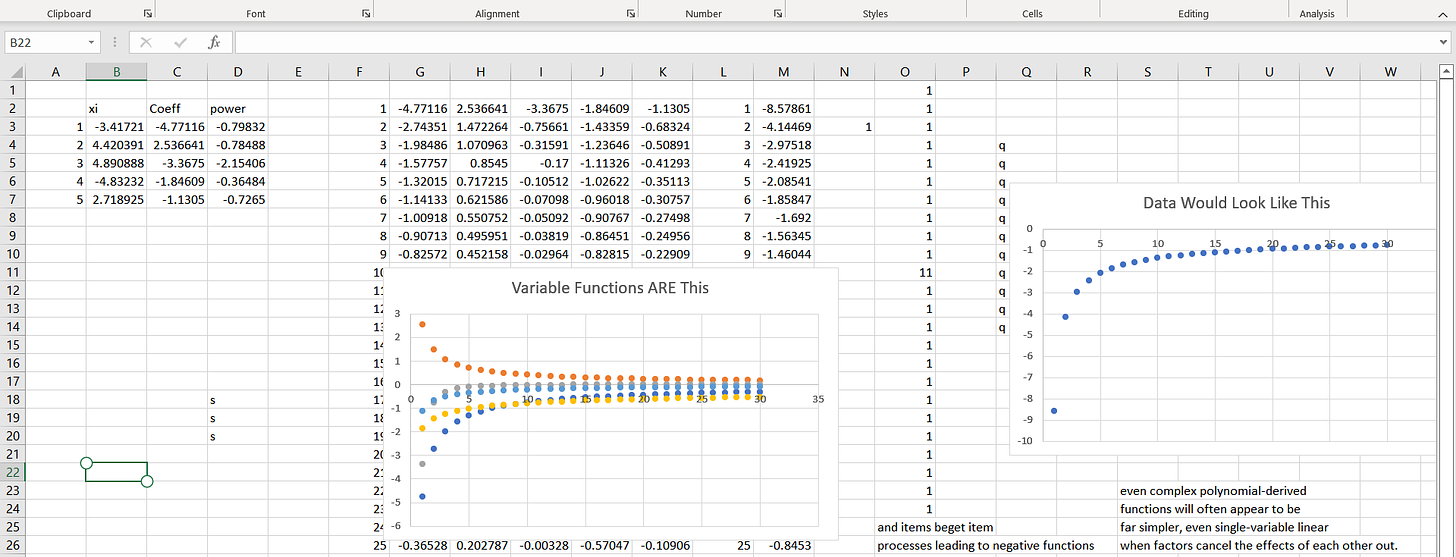
Look at this throw:

One variable appears to dominate (the right and left are nearly the same in scale) and yet four other real variables that each have their own, relatively smaller in scale, effect, would never be hinted at given the result on the right. Their smaller contribution, however, does not make them unimportant: a single bolt can hold an airplane together from falling out of the sky.

We may or may not know about the dominate variable; the measures of goodness of fit (R-squared, test of slope) may look just fine. Or we may not know about the variables with lower individual effect sizes, but they alone, or in combination, may be super-important for the overall process that generates the data.

Some of the truths underlying what appear to be very simple final data can be much more interesting. For example:

All of this points to a few facts that

• science as we have been doing it is entry-order sensitive;

• missing parameters cannot be extracted from convolved signals without knowing their fundamental influences prior to erecting a model, but the point of multiple regression is to erect a model, so it is not well-applied in most of the its uses.

This is why, since 2015, I have been harping on epidemiologists doing studies in public health to adopt objective model selection criteria - and to show all of their work, not just the final, polish, curve-fitted result.

Now, if you understand what you’re studying, you might have absolute prior knowledge of what variable data you should collect. That means it’s an explicit assumption that your model is not underspecified. How often does that happen? And how often do we test the correct form of a prediction model?

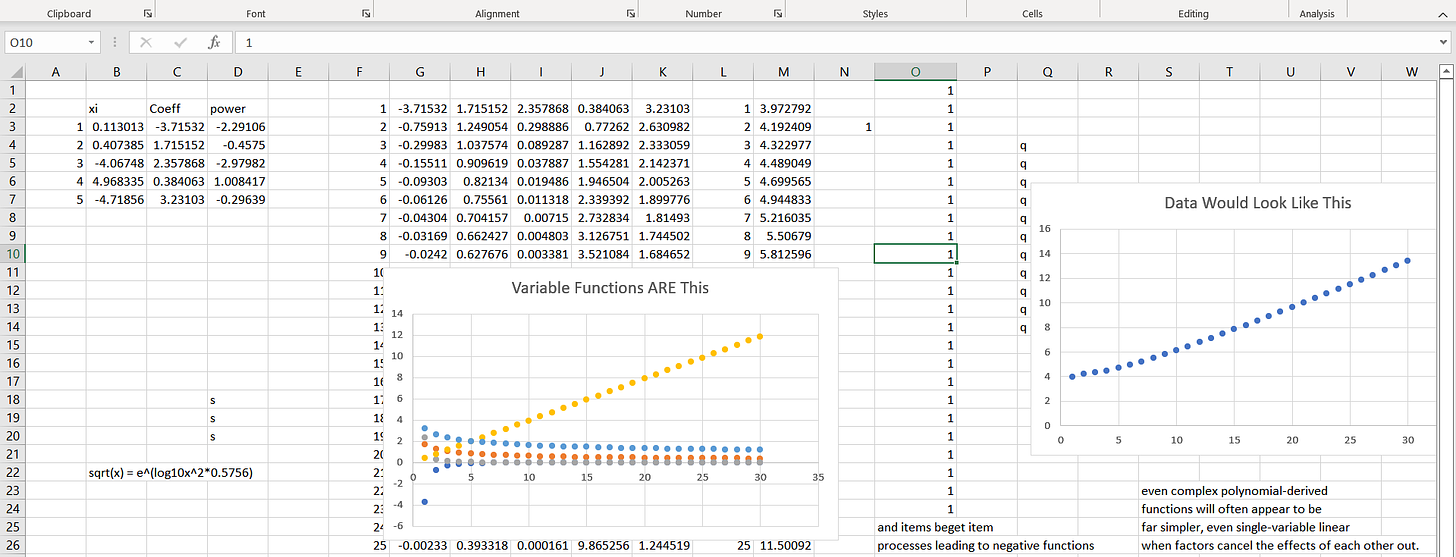
Not horrified yet? Here’s one that should make your skin crawl:

At least three of the individual functions are NEGATIVE and the resulting composite function is positive.

Note that we don’t need five inputs for this type of problem to exist.

Unknowns Exist

The unknowns often exist, too, perhaps as much as 90% of the time - and they can be absolutely lethal to your success in hypothesis testing about specific input variables and leave you with warped coefficients, well-fit models with poor generalizability.

Hundreds of thousands of students have studied multiple regression. Of these, many think ANCOVA can save you? No, they are methodological equivalents.

You’ve been curve-fitting, babe.

Interim Solution 1. Stop thinking that we can explain things using GLMs any better than we can using polynomials. Sure, we play it safe by not trying about exponents, but stop for a moment: aren’t they a real part of biological, psychological or sociological processes?

Interim Solution 2. Stop worrying about understanding functional relationships; misspecification is likely to throw you way off anyway. You can still focus on being able to be accurate in the model prediction. This involves new data, unseen by the models you’re creating to test generalizability.

Someone with more time than me might want to go back to old data sets studied with linear multiple regression, and derive models that are better fit using exponential regression… you’ll get a tighter fit, but the lesson of today is that model underspecification or mispecification can lead to horrendously far-off “understanding” with surprisingly good regression statistics. If interactions exist among independent variables, misspecification will warp their coefficients, too.

Here’s a video on exponential regression with a simple toy data set. It rather proves the point in that in the toy example, all inputs are assumed to be known, yet multiple regression is supposed to be useful in testing hypotheses of which inputs might be important.

https://stats.stackexchange.com/questions/151452/difference-between-regression-analysis-and-curve-fitting

Humanity needs to be able to predict better, and acknowledge that we risk more when we pretend to understand. Science is expensive, and errant models are even more costly.

In case you don’t recognize it, that’s the sound of a gauntlet being thrown. We can and must do better.

I have a solution to this terrific problem.

Someone like Stephen Wolfram or his team could create an AI model explorer that would systematically study expansive model space using x variables during a formal heuristic part of a study (Phase 1 model exploration). Standard measures are reported for thousands of models. During Phase 2, new data, completely unrelated to the data collected during Phase 1, can be used to test the reproducibility of the most promising classes of and individual models. Known functional relationships among independent variables are known, and each independent variable is checked for causal dependence on the dependent variable. Phase 2 can include more variables, but if the number of new variables is > x/3, the study drops back into Phase 1. Phase 2 can also tweak and update parameter estimates - which would be better estimated with combined data from Phase 1 and Phase 2 (once model selection is done!). The new data have then provided minor model adjustments and have provided the first parameter estimates we take seriously. Then, the predictions made using the models in Phase 2 are tested with one or more additional independent data sets and the accuracy, sensitivity in specificity of the final model are reported.

This is formal unsupervised machine learning in heuristic model exploration and supervised model parameter optimization. It’s man and machine working together. All of the steps are recorded and no one can cheat.

For all I know, this type of framework already exists and could be made easy enough to use by people in public health. I hope so.

Modern Esoterica Article #001. The Poverty of the Polynomial. (C) 2022 James Lyons-Weiler. Published on Popular Rationalism, Substack, 4/2/2022. This article or a version of it may or may not appear in the book, “Modern Esoterica”, expected in 2023. This article may not be reproduced in any form without permission of the author. Thank you!